论文：Models of Quantum Complexity Growth

Brandão, F. G. S. L., Chemissany, W., Hunter-Jones, N., Kueng, R., & Preskill, J. (2021). Models of Quantum Complexity Growth. PRX Quantum, 2(3), 1. https://doi.org/10.1103/prxquantum.2.030316

The paper provides a relation between the approximate designs and the quantum complexity.

Definition of the Quantum Complexity

Def 1 (Strong State Complexity): The complexity of a quantum state is the minimal circuit size required to implement an ancilla-assisted measurement that is capable of distinguishing from the maximally mixed state .

Pictographic illustration: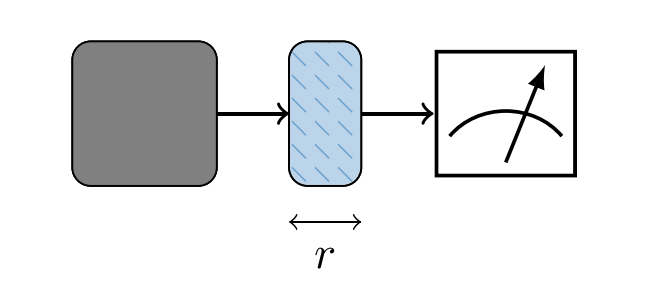

Black box: or .
Blue boxes: preprocessing circuits involving 2-local gates.

We say that the state has complexity less than if the probability of correctly distinguishing both states is close to optimal.
The optimal: $\beta{QC} (r,|\psi \rangle) \to 1-\frac{1}{d}|\psi \rangle\delta\beta{QC} (r,|\psi \rangle)\geq 1-\frac{1}{d} -\delta\mathcal{C}_\delta(|\psi \rangle)\leq r$.

Def 2 (Strong Unitary Complexity): The complexity of a quantum circuit U is the minimal circuit size required to implement an ancilla-assisted measurement that is capable of distinguishing from the completely depolarizing channel .

Pictographic illustration: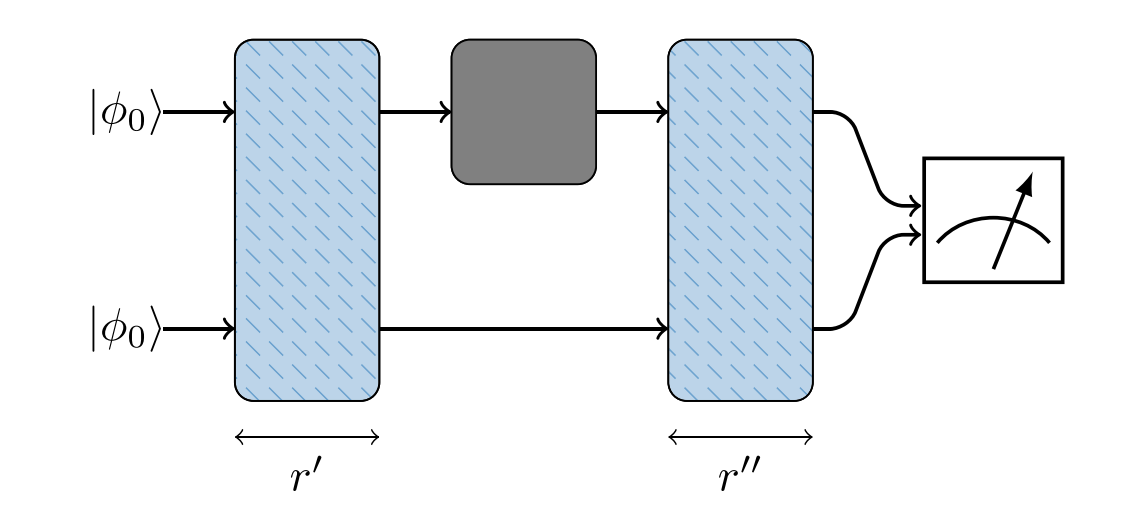

Black box: or operation on .
Blue boxes: pre- and postprocessing circuits involving and 2-local gates.

We say that the unitary has complexity less than if the probability of correctly distinguishing both options is close to optimal.
The optimal: $\beta{QC} (r,U) \to \frac{1}{2} |\mathcal U -\mathcal{D}|{\diamond} = 1-\frac{1}{d^2}, r \to \inftyU\delta\beta{QC} (r,U)\geq 1-\frac{1}{d^2} -\delta\mathcal{C}\delta(U)\leq r$.

Complexity by Design

Theorem 1 (State Complexity Growth): Consider the set of (pure) states in that results from applying all unitaries in an -approximate 2k-design to a fixed (but random) initial state . Then the set contains at least

$$\left(\begin{array}{c} d+k-1 \\ k \end{array}\right)\left[\frac{1}{1+\epsilon}-2 d(n+1)^{r}|\mathbf{G}|^{r}\left(\frac{16 k^{2}}{d(1-\delta)^{2}}\right)^{k}\right]$$

distinct states that obey each.
Qualitatively, the number is as long as r obeys .

Theorem 2 (Unitary Complexity Growth): A discrete approximate 2k-design in dimensions contains at least

$$\frac{d^{2 k}}{k !}\left[\frac{1}{1+\epsilon}-3 d^{2} n^{2 r}|\mathbf{G}|^{r}\left(\frac{1024 k^{4}}{d(1-\delta)^{2}}\right)^{k}\right]$$

distinct states that obey each.
Qualitatively, the number is as long as r obeys .